MATEMATICAS

COLEGIO MORALBA
ÁREA DE MATEMÁTICAS

 Bienvenidos

Bienvenidos al aula virtual de Matemáticas Moralba
Aquí encontrarás el plan de estudios, material de clase, e información para la clase de matemáticas.


PRIMER   TRIMESTRE


INDICADORES DE LOGRO

  1. Describe e interpreta propiedades y relaciones de los números naturales y sus operaciones.
  • Sistemas de numeración
  • Romano, binario
  • Números naturales
  • Operaciones y propiedades
  • Múltiplos y divisores
  • M.C.M. y m.c.d.
  • Ecuaciones de primer grado

 

  1. Resolver problemas que requieran encontrar y/o dar significado a la medida de tendencia central de un conjunto de datos
  • Conceptos básicos de estadística
  • Población, muestra, variables cualitativas y cuantitativas
  • Medidas de tendencia central
  • Moda
  • Media aritmética
  • Mediana

 

  1. Construir y descomponer figuras planas (triángulos y cuadriláteros) a partir de condiciones dadas.
  • Triángulos y cuadriláteros
  • Construcción con regla y transportador
  • Clasificación 
  • Ángulos.

 




Actividad No. 1

sistema de numeros shttps://www.colombiaaprende.edu.co/sites/default/files/files_public/contenidosaprender/G_6/M/M_G06_U01_L01/M_G06_U01_L01_01.html
Actividad No. 1
Realiza la marcación en tu cuaderno con "Segundo trimestre" y copia: Estandares basico de Competencia (EBC-DBA), Logros y  contenidos.

EBC-DBA
EBC: Utilizo números racionales, en sus distintas expresiones (fracciones, razones, decimales o porcentajes) para resolver problemas en contextos de medida.
DBA: Resuelve problemas que involucran números racionales positivos
EBC: Interpreto, produzco y comparo representaciones gráficas adecuadas para presentar diversos tipos de datos. (diagramas de barras, diagramas circulares.)
DBA: Relaciona información proveniente de distintas fuentes de datos.
EBC: Calculo áreas y volúmenes a través de composición y descomposición de figuras y cuerpos
DBA: Usa las fórmulas del perímetro, longitud de la circunferencia y el área de un círculo para calcular la longitud del borde y el área de figuras compuestas por triángulos, rectángulos y porciones de círculo


LOGROS
Reconoce diferentes representaciones de un mismo número y hace traducciones entre ellas
Representa gráficamente un conjunto de datos  e interpreta representaciones gráficas
Establece relaciones entre áreas y perímetros de figuras planas cuando se modifican las dimensiones de las figuras


CONTENIDOS
Números racionales positivos
-Fraccionarios
representación, orden, operaciones básicas
-Números mixtos y conversión
-Decimales
ubicación en la recta, orden, operaciones básicas.
-Cálculo exácto, estimación y aproximación.

Tablas y gráficos estadísticos
Recolección de información
Diagrama de árbol
Diagrama de barras.

Perímetros y áreas
Perímetro de polígonos y circunferencia
Áreas de polígonos y círculo

Perímetro y área de figuras compuestas.


NÚMEROS RACIONALES

ACTIVIDAD No. 2
1. Observar el siguiente video y realizar resumen  en el cuaderno.TEMA: Los números racionales, dura 15”,55 sg.
Video:  https://www.youtube.com/watch?v=GyZ0Q_s0S4U&t=757s

2.Contestar el formulario google..No. 1 Tema: Números racionales, no olvides dar click en enviar.
https://docs.google.com/forms/d/1niuYrOGJnQyKarMa1hWUofdQ_u2p9Thgg6f3doPpuis/edit

3.Registra la nota en tu cuaderno y  que tus  padres la firmen  y colócale  la fecha.

4.Si sacaste menos de 3,5 debes recuperar.


RECUPERACIÓN: Volver a ver el video y con la copia del formulario que le llegó  a su correo electrónico cuando presento del formulario de números racionales,  vuélvalo a resolver ahora correctamente.  Nuevamente que tus padres  firmen. Por ahora No es necesario enviar fotos.
                                                                                                           

EVALUACIÓN: Contestar el formulario google, que le llegará por medio de la plataforma Classroom, también llegará una copia a su correo electrónico con la nota y las preguntas.


Nota: Cada actividad realizada se le coloca un sello y vamos (4) Invéntate tu propia marca y lleva tus cuentas muy juicioso (a).
1. Marcación segundo trimestre.
2. Logros.
3. Resumen video números racionales.
4. Formulario impreso o copiado de números racionales.



NÚMEROS RACIONALES
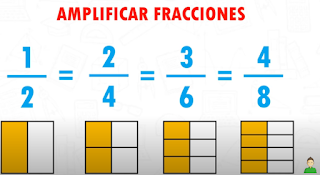
FRACCIONES

Actividad No.  3
Observa la siguientes diapositivas y copia las siguientes diapositivas


REPRESENTACIÓN UNA FRACCIÓN
Profesor Jair Andrés Castro Cuesta-Matemáticas





CLASIFICACIÓN DE LAS FRACCIONES
Profesor Jair Andrés Castro Cuesta-Matemáticas




                                                   EJERCICIOS DE FRACCIONES

Actividad No. 4
  Con base en la información anterior, contesta las siguientes preguntas.
a. ¿Que es una fracción?
b. ¿Cómo se representan las fracciones?
c. ¿Cómo se clasifican las fracciones?
d. Copia las siguientes fracciones en el cuaderno, escoge la respuesta correcta que representa, colorearla  y clasifícala.




e. Copia las siguientes fracciones en el cuaderno,  escribela, colorearla  y clasifícala (propia e impropia)





Actividad No.  5
Copia las siguientes fracciones y representa el fraccionario con color. ¿Se pueden volver fracciones mixtas? explica tu respuesta.


Actividad No. 6
 (PRIMERA PARTE)

AMPLIFICACIÓN, SIMPLIFICACIÓN E INTERPRETACIÓN DE FRACCIONES.

1.  Sacar  resumen en el cuaderno sobre cada video (simplificación y amplificación)
2.  Realizar los ejercicios del final del video.
3.  Contestar el  formulario Google: https://forms.gle/rqAqqws697EHeKWGA.
·         Indicaciones
  • No olvides dar click en enviar el formulario.
  • Después de enviarlo favor imprimirlo o copiarlo, debes tener evidencia del formulario en el cuaderno.
  • Si sacaste menos de 3,5, puedes volver a resolverlo.
  • La nota de su formulario llega directo a una hoja de Excel, no debes enviar evidencia de ello, tampoco de resúmenes, con el formulario se califica TODA la  actividad, pero si debes mantener el cuaderno al día.
AMPLIFICACIÓN DE FRACCIONES
VIDEO DE APOYO

Concepto: Amplificar una fracción es multiplicar el denominador y el numerador de una fracción, por el mismo número. 
Esta acción permite que tanto el denominador como el numerador de la fracción aumenten de valor tantas veces como se amplifica, pero el valor de la tracción como tal se mantiene igual y se denominan fracciones equivalentes.

Ejemplo No. 1






Ejemplo No. 2

Profesor Jair Andrés Castro Cuesta-Matemáticas





 SIMPLIFICACIÓN  DE FRACCIONES
VIDEO DE APOYO


CONCEPTO:
Simplificar es reducir la fracción a la mínima expresión, dividiéndola en los números primos  que son 2,3,5,7,11, pero debemos dividir tanto numerador como denominador por el mismo número primo.
En la simplificación las fracciones se hacen mas pequeñas, pero en representación es la misma
Cuando simplificamos las fracciones se hacen  mas pequeñas, pero  tienen el mismo valor.
Como resultado de la simplificación nos dan fracciones equivalentes.


Profesor Jair Andrés Castro Cuesta-Matemáticas




ACTIVIDAD No. 6  SEGUNDA PARTE
Juego de amplificación y simplificación de fracciones.
https://www.smartick.es/matematicas/exercise.html?resource=simplificar-Fracciones-I



Nota: Te sale una pantalla interactiva así, debes realizar 20 ejercicios y copiarlos en el cuaderno.




Actividad No. 7 
NÚMERO MIXTO
Los números mixtos o fracciones mixtas son los números quebrados que se conforman con un número entero y una fracción, que obligadamente tiene que tener un numerador menor al denominador.
Todo número mixto está formado por dos partes:
Un número entero y Una fracción propia.
Los números fraccionarios generalmente se conforman con números positivos, pues los números negativos producen resultados contrarios.





La lectura de estos números tiene un orden de lectura y debe también aclararse que los números mixtos se convierten en fracciones impropias como se muestra en la siguiente operación de la imagen.


Fuente: https://www.ejemplode.com/5-matematicas/1362-ejemplo_de_numero_mixto.html#ixzz6LgLLuo4l



SEGUNDO TRIMESTRE


Actividad No. 8 
La actividad corresponde a la semana del  18 de mayo 2020
Ver  el video explicativo sobre número mixto
 
Evaluación  de la actividad mediante la resolución de un formulario google
https://forms.gle/xgP6xDfvg56BEavq6 


   
      Actividades:
1. Sacar  resumen en el cuaderno sobre el video: Número mixto.
2. Realizar los ejercicios del final del video.
3. Contestar el  formulario Google.
·          

Indicaciones
  • No olvides dar click en enviar el formulario.
  • Después de enviarlo te va a salir la opción, ¿Quieres copia de tu formulario?  dile que   sí, porque lo debes tenerlo en tu cuaderno, sea copiado o impreso.
  • Si sacaste menos de 3,5, favor enviar foto por Classroom del formulario     corregido y   explicando cada respuesta.
  • La nota de su formulario llega directo a una hoja de Excel, no debes enviar evidencia de ello, tampoco de resúmenes, con el formulario se califica TODA la  actividad, pero si debes mantener el cuaderno al día., Vamos 7 Sellos así:
Nota: Cada actividad realizada se le coloca un sello y vamos (7) Invéntate tu propia marca y lleva tus cuentas muy juicioso (a).

1. Marcación segundo trimestre.
2. Logros.
3. Resumen video números racionales.
4. Formulario impreso o copiado de números racionales.
5. Resumen video número mixto.
6. Ejercicios que quedan al final del video.
7. Formulario de número mixto, sea pegado o impreso.




Actividad No. 9 

"Vamos a Jugar"

 Adjunto 2 links donde podemos hacer ejercicios de fracciones equivalentes.

PRIMER LINK
https://www.mathgames.com/skill/3.44-make-equivalent-fractions


 SEGUNDO LINK
https://www.mathgames.com/skill/3.45-choose-the-equivalent-fraction

Es solo para practicar...............no hay que realizar ningún envío. ¿Cuantas estrellitas ganaste?





Actividad No. 10
1. Observar los siguientes videos
2. Sacar resumen de cada video y hacer los ejercicios planteados al final.
3. Realizar lectura de La recta numérica y fracciones en la recta, para aclarar el concepto.
4. Resolver el formulario google.


Ubicar una fracción en una recta   2´25 sg

Ubicar varias fracciones en una recta 2´30 sg



 LA RECTA NUMÉRICA
Recta: Una recta es una línea de una sola dimensión que está compuesta por una sucesión infinita de puntos, prolongada en una misma dirección.
Numérico: por su parte, es un adjetivo que se refiere a lo que está vinculado a los números (los signos que expresan una cantidad).




Recta numérica
Se trata de la línea en la cual se suelen graficar los números enteros como puntos que están separados por una distancia uniforme.
De este modo, la recta numérica facilita la suma y la resta, resultando muy útil cuando se desea enseñar estas operaciones a alguien.
La recta numérica también se conoce con el nombre de recta real, ya que se trata de una línea recta en la cual es posible encontrar el conjunto de los números reales, dentro del cual podemos ubicar los racionales (el cero, los negativos y los positivos) y los irracionales (aquellos que no pueden expresarse mediante una fracción m/n, siendo ambos componentes números enteros y n, mayor o menor a cero).


                                   FRACCIONES EN LA RECTA NUMÉRICA

Representación de  fracciones en la recta numérica:

Para ubicar fracciones en la recta numérica se divide la unidad (entero) en segmentos iguales, como indica el denominador, y se ubica la facción según indica el numerador.
Si la fracción no es unitaria en la recta numérica se realiza el mismo procedimiento, es decir, se divide el entero en partes iguales según lo que indique el denominador de la fracción. Luego, se ubica la fracción en el segmento que está señalado en el numerador.

Ejemplo 1 Representar en la recta numérica: 5/3  y  7/2 

Solución.

Profesor Jair Andrés Castro Cuesta-Matemáticas





Profesor Jair Andrés Castro Cuesta-Matemáticas




Actividad No.  11
Representa las  siguientes fracciones en la recta numérica. 
Explicación: Realiza la actividad en tu cuaderno, no olvides, primero debes sacar el numero fraccionario (número racional) correspondiente a las siguientes gráficos, después dibujar la  recta numérica y por ultimo ubicarlo.



http://www.seg.guanajuato.gob.mx/sde/dmme/matemticas/6o%20primaria.pdf




Actividad No.  12
Número decimales  a fracciones
VIDEO DE APOYO 7¨56 Sg
https://www.youtube.com/watch?v=mB5d5Q-YgxI

Para convertir un número decimal a fracción, debemos tener en cuenta que del punto a la derecha, los numero se llaman DECIMALES  y tienen diferentes nombres según su posición así:




Ejemplo


Actividad No.  13
Clasificación de las fracciones
Profesor Jair Andrés Castro Cuesta-Matemáticas


Operaciones de suma y resta con fracciones homogéneas
Profesor Jair Andrés Castro Cuesta-Matemáticas

Operaciones de suma y resta con fracciones heterogéneas






REPASO SUMA Y RESTA  DE NÚMEROS DECIMALES




TANGRAM VIRTUAL


PLAN DE MEJORAMIENTO 

DESCRIPCIÓN DE ACTIVIDADES:
1.Realizar en el cuaderno, a color 5 ejemplos del TANGRAM VIRTUAL


2.Repasar las actividades realizadas durante éste segundo trimestre, que se encuentran en el blog. https://aulavirtualmaritzamayorlopez.blogspot.com/p/matematicas_14.html.
Actividad No.  2 Números racionales
Actividad No. 6 Amplificación, simplificación e interpretación de fracciones.
Actividad No. 8 Numero mixto.

No es necesario enviar evidencias, al contestar el siguiente formulario se evalúa toda la actividad:
FORMULARIO:



TERCER TRIMESTRE

logros tercer trimestre

LOGROS

·         Resolver y formular problemas sencillos de proporcionalidad directa.

·         Hace traducciones entre diferentes representaciones de un conjunto de datos para dar solución a un problema.

·         Resuelve problemas que requieren de la construcción de moldes para cubos, cajas, prismas o pirámides dadas sus dimensiones y justifica cuando cierto molde no resulta válido para la solución de dicha situación.

 

CONTENIDOS

Razones y proporciones

Noción de razón y proporción

Proporción directa

Porcentajes

Números negativos

 

Diagramas estadísticos

Diagrama circular

Construcción de diagrama circular con regla y transportador.

 

Sólidos geométricos

Cilindros, cubos, prismas, pirámides.

Representación bidimensional

Construcción de moldes.

área de superficie y volumen de una caja.





MARCO TEÓRICO Y ACTIVIDADES
COLEGIO MORALBA SUR ORIENTAL I.E.D.
GRADO

ASIGNATURA
MATEMATICAS


Guía N°

REALIZAR EN LA SEMANA DEL
12 DE AGOSTO AL 4 DE SEPTIEMBRE











INDICADORES DE LOGRO: Resuelve y formula problemas sencillos de proporcionalidad directa e inversa
TEMA: problemas relacionados con razones y proporciones. (proporción directa)

MARCO TEÓRICO:
Encontraras información relacionada sobre este tema en : https://www.portaleducativo.net/septimo-basico/293/Razones-proporciones
1- Razón
Una razón es una comparación entre dos o más cantidades. Puede expresarse mediante una fracción. Si las cantidades a comparar son a y b, la razón entre ellas se escribe como:








Ejemplo 1:
En una sala de clases hay 10 mujeres y 18 hombres. ¿Qué relación numérica existe entre el número de mujeres y el número de hombres?

La relación entre el número de mujeres y el número de hombres es de ”10 es a 18”, otra forma de leerlo es "10 a 18 " de aquí también se puede concluir que por cada 5 hombres hay 9 mujeres

El término a es el antecedente de la razón y el b, el consecuente.









El resultado de la división o cociente entre el antecedente y el consecuente se denomina valor de la razón





Dos o más razones son equivalentes cuando tienen igual valor.
En el caso anterior 10 hombres/18 mujeres = 0.55555…
                                  5 hombres/9 mujeres = 0.55555…hombres/mujeres
Luego la razón 10 es a 18 es equivalente a la razón 5 es a 9
Se lee 10 es a 18 como 5 es 9


Ejemplo 2.









La razon 5 es a 13  …………………………es la misma que 25 es a 65

Ejemplo 3
De 2000 pruebas para covid realizadas, 1500 salen negativas y 500 positivas
Quiere decir que la  razon entre el numero de resultados positivos  y el numero de reusultados negativos es de 500 a 1500
500 positivos /1500     negativos
O de 1 positivo/3  negativos  (dividiendo numerador  y denominador por 500)
Por cada resultado positivo hay 3 resultados negativos.

Ejemplo 4
Si cada  8 dias el numero de contagios por covid aumenta en 800, entonces la razon entre el numero de contagios y el numero de dias  es de 800 a 8
 800 contagios/ 8 dias
100 contagios /1 dia
Hay 100 contagios por dia en promedio.

Ejemplo 5
Un automovil recorre 600 kilometros en 12 horas. Entonces la razon entre el numero de  kilometros recorridos y el numero de horas es de 600 a 12.
600 kilometos/ 12 horas  
50 kilometrros/ 1 hora      (dividiendo el numerador y el denominador en 12)
En este caso la razon entre la distancia recorrida con relacion al tiempo empleado se denomina velocidad media.
NOTA: Todas la razones cuyo denominador sea una unidad de tiempo( segundos, minutos, horas, dias,…) se denominan razones de cambio.

Ejemplo 6
En 1000 minutos de juego Cristiano Ronaldo marco 60 goles, la razon entre el nuimero de goles y el tiempo es de 60 a 1000
60 goles/1000 minutos, otras razones equivalentes  son
30 goles/500 minutos
15goles/250 minutos
3 goles/125 minutos
3 goles/125 minutos              marca 3 goles cada 125 minutos
1/41,66666                               marca un gol cada 41,666 minutos



ACTIVIDADES RESUELTAS DE RESOLUCIÓN DE PROBLEMAS:
Podrás encontrar videos relacionados en el siguiente enlace:

https://www.youtube.com/watch?v=jboHWe4_6D8    Razones y proporciones solución de problemas | Ejemplo 1

https://www.youtube.com/watch?v=ktY7MZ4TD3E  Resolver problemas con razones

Veamos cómo resolver problemas de razones:

Problema 1



Por cada taza de café agregar 3 cubos de azúcar.
¿Cuántos cubos de azúcar se agregan a 5 tazas de leche?
   
           
En este caso se pueden realizar varios procedimientos
a. Sumar 3+3+3+3+3= 15   (para la primera taza agregamos 3, para la segunda otros  3, para la tercera otros 3…)
b. Multiplicar 5x3 = 15       (5 veces tres)
c. Regla de tres

En este caso se realiza una igualdad de razones, como a una taza de café le corresponden tres cubos de azúcar la razón queda 1taza de café/3 cubos de azúcar
Como no sabemos cuántos cubos de azúcar a corresponden a 5 tazas la razón queda 5 tazas de café/X cubos de azúcar

Igualando las expresiones propuestas queda         

                            1/3= 5/X                                           

Que se lee de la siguiente manera
1 es a 3 como 5 es a X
también se puede leer asi
1 dividido en 3 es igual a 5 dividido en X.

Despejando X = (3 por 5) /1   equis es igual a la multiplicación de 3x5 dividido en 1
 
X= 15/1
X= 15
se necesitan 15 cubos de azúcar.


d. Construcción de tabla
  
Numero de tazas de café Numero de cubos de azúcar
1 3
2 6
3 9
4 12
5 15
6 18


     









En la tabla se observa que para 5 tazas de café se necesitan 15 cubos de azúcar

Problema 2.
Las edades de 2 personas están en la relación de 5 a 9 y la suma de ellas es 84. Hallar las edades.

Solución1:
Si las edades son a y b
Cuando nos hablan de relación o razón entre dos cantidades sabemos que nos están hablando de una comparación entre dos cantidades. Por lo tanto expresamos los datos como una razón:






Ahora volvemos a los datos del problema:

Nos indican que la suma de los 2 números nos tiene que dar 84. Esto se expresa así:






 podemos así trabajar con una constante, que en este caso será " X" . Por lo tanto:




El valor del número” a” Equivale a 5 multiplicado por un número desconocido X.
El valor del número” b” Equivale a 9 multiplicado por un número desconocido X
El numerador se lee cinco multiplicado por equis o cinco equis
El denominador se lee nueve multiplicado por equis o nueve equis
Reemplazando los datos construimos las siguientes ecuaciones:
Primera ecuación:      a + b = 84      (porque sabemos que la suma de los números da ochenta y cuatro)
Segunda ecuación: 5X + 9X = 84      ( reemplazando los valores de “a” y “b”)
así 14X = 84  ( sumando cinco equis más nueve equis da catorce equis)                                                                                   
Debemos hallar un numero X que multiplicado por 14 dé como resultado 84
Para hallar este valor dividimos 84 entre 14
Luego la equis es igual a 84 dividido en 14                                                       X = 84∕ 14
 
La X es igual a 6                                                                                                      X = 6
Con el valor de X =6 podemos hallar el número “a” y el numero “b”
Así multiplicando 5 por 6                                                      5 por 6 = 30          ( 30 es el valor de “a”)
Del mismo modo multiplicando 9 por 6                            9 por 6= 54           (54 es el valor de “b”)
Se cumple que   30+54=84
Las edades de 2 personas están en la relación de 5 a 9 y la suma de ellas es 84. Hallar las edades.
Solución: una edad es 30 y otra edad es 54
Porque 5/9 = 30/54
Solución 2
Construyendo una tabla de las posibles edades de “a”  y de “b” sabiendo que las edades de “a” son múltiplos de 5 y las de “b” son múltiplos de 9

Edad de a Edad de b Suma de las edades
5 9 14
10 18 28
15 27 42
20 36 56
25 45 70
30 54 84
 35 63 98
En la tabla se observa que las únicas edades que suman 84 son 30 y 54.


Problema 3
Solución 1:
Dos numeros mantienen una razon de 18 a 15, si el mayor de ellos es 24 ¿Cuál es el otro?
En este caso se puede plantear una igualdad entre las dos razones y designar al numero desconocido por la letra X, como se observa en la siguiente imagen.




24 es a X como 18 es a 25
Para saber que valor tiene la X se multiplican los valores extremos 24 y 15  y luego este resultado se divide entre el 18 que es uno de los valores medios.
Continuando con el proceso podemos simplificar tanto el numero 24 ( en el numerador) como el numero 18 (en el denominador) dividiendo cada uno en 6.
Y despues de realizar las divisiones la incognita X queda igual  a:
              4 x 15
 
X =   ---------------
                   3
X= 60/ 3                              realizando operaciones en el numerador
X= 20                                    dividiendo 60 en 3

Respuesta:
Dos numeros mantienen una razon de 18 a 15, si el mayor de ellos es 24 ¿Cuál es el otro?
El otro número es 20


Solución 2.
Construyendo una tabla
Para construir la tabla simplificamos la razón 
Número menor / número mayor = 15/18
Tanto el 15 como el 18 se pueden dividir en 3
Luego la razón 15/18 es igual a la razón 5/6
Número menor Número mayor
5 6
10 12
15 18
20 24
25 30
30 36
35 42











Para construir la tabla se multiplica cada término de la razón por 1, luego por 2, luego por 3, luego por 4, luego por 5, luego por 6
Y así los números de la columna del número menor corresponde a múltiplos de 5 y la columna del número mayor corresponde a múltiplos de 6.


Para reflexionar:
La formulación, el tratamiento y la resolución de los problemas suscitados por una situación problema permiten desarrollar una actitud mental perseverante e inquisitiva, desplegar una serie de estrategias para resolverlos, encontrar resultados, verificar e interpretar lo razonable de ellos, modificar condiciones y originar otros problemas. Es importante abordar problemas abiertos donde sea posible encontrar múltiples soluciones o tal vez ninguna. También es muy productivo experimentar con problemas a los cuales les sobre o les falte información, o con enunciados narrativos o incompletos, para los que los estudiantes mismos tengan que formular las preguntas. Más bien que la resolución de multitud de problemas tomados de los textos escolares, que suelen ser sólo ejercicios de rutina, el estudio y análisis de situaciones problema suficientemente complejas y atractivas, en las que los estudiantes mismos inventen, formulen y resuelvan problemas matemáticos, es clave para el desarrollo del pensamiento matemático en sus diversas formas. (MEN, EBC, 2005)


ACTIVIDADES:
A continuación, encontraras un cuestionario tipo ICFES, la actividad consiste en construir y desarrollar un plan o estrategia para resolverlos y escoger una de las 4 pociones de respuesta.

1.       Un almacén ofrece una promoción: compre 3 camisetas por $10.000, esto quiere decir que una persona que quiera comprar 5 camisetas debe tener al menos:
A.       $13.000
B.       $16.000
C.       $19.000
D.       $22.000
2.       Un mapa está construido con la siguiente razón: 1cm /500 metros (un centímetro en el dibujo equivale a 500 metros en la realidad) Si en el mapa la distancia entre A y B es 7,6 cm.
En la realidad esta distancia es:
A.       3400 metros
B.       3600 metros
C.       3800 metros
D.       4000 metros
3.       La razón entre las edades de Andrés y Beatriz es de 3 a 4, si la edad de Andrés es 12 años la edad de Beatriz es:
A.       13 años
B.       14 años
C.       15 años
D.       16 años

LAS PREGUNTAS 4, 5, 6 ,7 Y 8 CORRESPONDEN A LA SIGUIENTE TABLA, SABIENDO QUE SE CUMPLE EN CADA FILA LA MISMA RAZON.

Número de pruebas de covid 19
Resultados positivos
Resultados negativos
200
30
170
400
60
340
600
X
510
800
120
680
1000
150
Y
1400
Z
W
 
4.       El valor de” X” es:
A.       70
B.       80
C.       90
D.       100
 
5.       El valor de “y “es:
A.       750
B.       850
C.       950
D.       1050
 
6.       EL valor de “Z” es:
A.       180
B.       190
C.       200
D.       210
 
7.       EL valor de “W” es:
A.       920
B.       1020
C.       1120
D.       1220
 
8.       La razón entre los casos negativos y positivos es:
A.       3/15
B.       15/3
C.       3/17
D.       17/3
 
9.       Un tubo de 3 metros de largo es cortado en dos secciones cuya razón es de 3 a 7.  Por lo tanto, la medida de la sección más corta es:
A.       90 centímetros
B.       100 centímetros
C.       110 centímetros
D.       120 centímetros.
 
10.    Para aliviar los síntomas de un resfriado, un médico formula 2 pastilla de acetaminofén, 1 de ibuprofeno y 3 sobres de antigripal al dia, durante 10 días. Si al ir a la farmacia solamente hay dos sobres de acetaminofén cada uno de 8 pastillas, un sobre de ibuprofeno de 6 unidades y 20 sobre de antigripal. La cantidad de días que quedara sin recibir la dosis completa, diaria serán:
A.       3
B.       4
C.       5
D.       6



PASATIEMPOS Y PROBLEMAS VARIOS QUE POTENCIAN EL PENSAMIENTO LÓGICO MATEMÁTICO
  1. dibuje un cuadrado con tres líneas.
  2. coloque 5 vacas en los seis espacios siguientes sin que sobre o falte espacio alguno









  1. ¿qué pregunta le harías a un dado que tiene tres caras con la palabra SI y tres con la palabra NO, para que, sin importar el resultado del dado, lo que arroje sea verdad? Si sale SI la respuesta sea correcta, si sale NO la respuesta también sea correcta.
  2. Ordene las letras para que se forme el nombre de una ciudad de Colombia
a.        IALC
b.       NOTIMERA
c.        GRANACATE
d.       ACELITI
e.       NAGUCAMABRA
  1. Escriba el elemento que sigue en cada secuencia.
a.        2,4,6,8,10.
b.       1,3,5,7,9,
c.        1,1,2,3,5,8,13,21,
d.       U,D,T,C,C,S,T
e.       L,M,M,J,V,S,


EVALUACIÓN
  1. Responda y describa el proceso que utilizo para hallar la solución de cada uno de los puntos del cuestionario tipo ICFES
  2. De solución a cada uno de los 5 puntos de los pasatiempos y problemas varios que potencian el desarrollo del pensamiento lógico matemático justificando cada respuesta.
  3. Realice una auto evaluación de lo aprendido
4. Conteste las preguntas en el formulario que se encuentra al inicio.



EVALUACIÓN: ENVIÉ SUS RESPUESTAS DE LA CARTILLA AL SIGUIENTE FORMULARIO:  Link del formulario de Google https://forms.gle/yPT6VA77moyFv4Mz8
CARTILLA No. 1
GUÍA No. 2
EVALUACIÓN: ENVIÉ SUS RESPUESTAS DE LA CARTILLA AL SIGUIENTE FORMULARIO:  Link del formulario de Google :https://forms.gle/CPYDMGwMtm2zF8Yi8





MARCO TEÓRICO Y ACTIVIDADES


COLEGIO MORALBA SUR ORIENTAL I.E.D.
GRADO

ASIGNATURA
MATEMÁTICAS


Guía N°

REALIZAR EN LA SEMANA DEL
7  DE SEPTIEMBRE AL 25 DE SEPTIEMBRE










INDICADORES DE LOGRO: Resuelve y formula problemas sencillos de proporcionalidad directa e inversa
TEMA: problemas relacionados con razones y proporciones. (proporción directa e inversa, regla de tres)
MARCO TEÓRICO:






La proporción indica mediante una igualdad la comparación de dos razones. Para escribir una proporción, debemos tener en cuenta que los valores antecedentes, siempre estén del mismo lado, al igual que los consecuentes.
En nuestro ejemplo del salón de clases, podemos comparar la razón que tenemos, de 4 niñas por cada 3 niños, y podremos calcular cuántos niños hay en un salón en relación al número de niñas o viceversa. 
 
Para esto, en primer lugar, escribiremos la proporción que ya conocemos:
4:3
Después, un signo de igualdad
4:3=
Y después la cantidad total, por ejemplo, la del mismo salón, recordando que debemos respetar el orden del antecedente y del consecuente. En nuestro ejemplo, el antecedente será el número de niñas, y el consecuente el número de niños.
4:3=24:18
 
Para comprobar la igualdad de la proporción, se efectúan dos multiplicaciones. En una proporción, tomaremos como referencia el signo de igualdad. Los números que están más cercanos, se llaman centros, y los números más lejanos son los extremos. En nuestro ejemplo, los números 3 y 24 son los más cercanos al signo igual, por lo que son los centros. El 4 y el 18, son los extremos. Para comprobar que la proporción es correcta, el producto de la multiplicación de los centros debe ser igual al producto de la multiplicación de los extremos:
3 X 24 = 72
4 X 18 = 72


Videos relacionados con el tema de proporciones:

https://www.youtube.com/watch?v=0jUM-p1QyOE   Qué es una proporción EJEMPLOS


https://www.youtube.com/watch?v=jboHWe4_6D8  Razones y proporciones solución de problemas | Ejemplo 1



Observe que el producto de 3 por 20 es igual al producto de 4 por 15
“en una proporción directa el producto de los medios es igual al producto de los extremos”
En este caso los extremos son el 3 y el 20. Y los medios son el 4 y el 15




Recuerde que las razones se diferencian de las fracciones porque las razones pueden invertir el orden de las cantidades mientras que las fracciones no.
Al referirnos al ejemplo anterior se puede observar que:
1 taza de arroz es a 2 tazas de agua se puede escribir 1 taza de arroz/2tazas de agua = 1/2
Es lo mismo que
2 tazas de agua es a 1 taza de arroz se puede escribir como 2tzas de agua / 1 taza de arroz= 2/1
De otro lado si fueran fracciones no será lo mismo escribir ½ que 2/1








PROPORCIÓN DIRECTA Y PROPORCIÓN INVERSA
Proporción directa: cuando aumenta una magnitud también aumenta la otra.
Ejemplo 1.
un pasaje cuesta $2400, 2 pasajes cuestan $4800, 3 pasajes cuestan $7200…
A medida que aumenta la cantidad de pasajes aumenta el costo de los pasajes
Las proporciones pueden expresar relaciones en que el aumento de la cantidad del antecedente aumenta la cantidad del consecuente. A esta variación se le llama proporción directa. El ejemplo anterior es una proporción directa.
Proporción inversa: En una proporción inversa, el aumento de la cantidad en una magnitud, significa la disminución de la cantidad en la otra.
Ejemplo 2
50 obreros construyen una casa en 20 días, entonces 100 obreros construirán la misma casa en 10 días…
A medida que aumenta el número de obreros se disminuye el tiempo de construcción de la misma casa.
 Si aumenta al doble el número de obreros, el tiempo disminuye a la mitad.


Ejemplo 3
 en una mueblería, 6 trabajadores hacen 8 sillones en 4 días. Si queremos saber cuántos trabajadores se necesitan para construir los 8 millones en 1, 2 y 3 días, usaremos una proporción inversa.
Para determinarla, usaremos el número de trabajadores como cifra antecedente, y el número de días como cifra consecuente:
6:4=
Siguiendo el mismo orden, del otro lado de la igualdad tendremos como antecedente nuevamente el número de trabajadores, y como consecuente los días que tardarán. Tendremos algo Como lo siguiente:
6:4 = ?:3
6:4 = ?:2
6:4 = ?:1
Para determinar la proporción inversa, multiplicaremos los factores de la razón conocida, en nuestro ejemplo, 6 y 4, y el resultado lo dividiremos entre el dato conocido de la segunda razón. Así, en nuestro ejemplo, tendremos:
6 X 4 = 24
24 / 3 = 8
24 / 2 = 12
24 / 1 = 24
Así tendremos las proporciones siguientes:
6:4 = 8:3
6:4 = 12:2
6:4 = 24:1
Con lo que podemos calcular que, para producir los 8 sillones en 3 días, necesitamos 8 trabajadores;
para fabricarlos en dos días, necesitamos 12 trabajadores, y para hacerlos en 1 día, necesitamos 24 trabajadores.

Fuente: https://www.ejemplode.com/5-matematicas/1289-ejemplo_de_razones_y_proporciones.html#ixzz6SMhjEelm


 
 
Problemas de proporciones:
Proporción directa:

1. En un colegio por cada 3 mujeres hay 2 hombres   si hay 600 mujeres, ¿Cuántos hombres hay en el colegio?

Se puede escribir siguiente proporción
3mujeres / 2 hombres = 600/ X            tres mujeres es a dos hombres como 600 es a X, donde X es el número de hombres

3 por X es igual a 2 por 600                porque el producto de los extremos es igual al producto de los medios

3X= 1200                                    porque 3 por equis es igual a tres equis y dos por seiscientos es igual a mil doscientos.
X= 1200/ 3                                   el valor de X es igual a 1200 dividido en 3

X= 400                                              hay 400 hombres
 


2. En una fiesta se invitaron a niños y niñas. Si sabemos que acudieron en una proporción de 6 niñas por cada 4 niños, y en la fiesta hay 32 niños ¿Cuántas niñas fueron?

6:4 = X :32                       6 es a 4 como X es a 32, es la proporción indicada en el problema. X representa  la cantidad de niñas.
 
6 por 32 = 192                es el producto de los extremos                 
4 por X es el producto de los medios

192 = 4X                        el producto de los extremos  es igual al producto de los medios
192/4 =X                 el valor de la X es igual a la división de 192 dividido en 4,
 
No importa que la letra X quede en la parte derecha de la igualdad.
48 = X                            hay 48 niñas
Hay 32 niños y 48 niñas.



3. Para armar una mesa, se necesitan 14 tornillos. ¿Cuántos tornillos necesitamos para armar 9 mesas?

14:1 = X :9                     14 tornillos es a 1 mesa como   equis tornillos es a 9 mesas  (X es el numero de tornillos)
 
14 por 9 = 126               es el producto de los extremos   
1 por X es el producto de los medios
 
126= 1por X                 el producto de los extremos es igual al producto de los medios
126/1 =X                      126 dividido en 1 es igual a X

126 = X                           126 son los tornillos son necesarios. Para las 9 mesas. 

Observe que se cumple la proporción 14:1 = 126:9 (14 es a 1 como 126 es a 9)
 
 
4. Las longitudes en un mapa y las longitudes reales que este representa son directamente proporcionales. Por ejemplo, si
en el mapa la distancia de A a B es cuatro veces más que la distancia de A a C, entonces, en la realidad, la distancia de A’ a
B’ es cuatro veces más que la distancia de A’ a C’.





Proporción inversa:
1. Dos grúas mueven 50 contenedores 90 minutos ¿Cuántas grúas se necesitan para mover los 50 contenedores en 30 minutos?
En este caso para bajar el tiempo se requieren más grúas, luego hay que construir una proporción inversa, porque cuando una magnitud disminuye la otra aumenta.
2: 90 = X: 30               2 grúas es a 90 minutos como equis grúas es a 30 minutos.
2 por 90 = X por 30         en las relaciones inversas el producto de los valores del lado izquierdo de la igualdad es igual al producto de los valores del lado derecho de la misma.
180 = X por 30                            
180/30 = X                  despejando el valor de X
6    = X                    se requieren 6 grúas, para mover los 50 contenedores en 30 minutos. 
  1. Si 4 alumnos realizan un trabajo en equipo en 45 minutos ¿Cuánto tiempo tardarán si el equipo está formado por 6, 8, 10 y  12 estudiantes?
                Tendremos las siguientes proporciones inversas:
a)      4:45 = 6:X                     4 estudiantes es a 45 minutos como 6 estudiantes es a  equis minutos
b)      4:45 = 8:X                     4 estudiantes es a 45 minutos como 8 estudiantes es a  equis minutos
c)      4:45 = 10:X                   4 estudiantes es a 45 minutos como 10 estudiantes es a  equis minutos                                                   
d)     4:45 = 12:X                    4 estudiantes es a 45 minutos como 12 estudiantes es a  equis minutos                  
teniendo en cuenta que el producto del lado derecho es igual al producto del lado izquierdo de la igualdad, y luego despejando el valor de la equis, los tiempos serán iguales a:
a)      180 / 6 =  X                                                               6 estudiantes tardaran 30 minutos
b)      180 / 8 = X                                                                8 estudiantes tardaran 22.5 minutos
c)      180 / 10 = X                                                              10 estudiantes tardaran 18 minutos
d)     180 / 12 = X                                                               12 estudiantes tardaran 15 minutos
Por lo que las proporciones serán:
a)      4:45 = 6:30
b)      4:45 = 8:22.5
c)      4:45 = 10:18
d)     4:45 = 12:15
3.   
Se necesitan 600 tejas para cubrir el tejado. Entre más trabajadores hagan el trabajo, menos tejas tendría que poner cada
uno. El número de trabajadores es inversamente proporcional al número de tejas que coloca cada trabajador. Por ejemplo,
cuando el número de trabajadores se duplica, el número de tejas por trabajador se divide por 2.





# de
trabajadores
# de tejas por
trabajador
1
600
2
300
3
200
50
12
60
10
Observe lo siguiente: al multiplicar horizontalmente los datos de cada fila da siempre 600

1 × 600 = 600
2 × 300 = 600
3 × 200 = 600r
50 × 12 = 600
60 × 10 = 600
Además, si las cantidades de una columna aumentan las cantidades de la otra disminuyen
Fuente: https://www.ejemplode.com/5-matematicas/1289-ejemplo_de_razones_y_proporciones.html#ixzz6SMiqThwn

Para reflexionar:
“un ser humano por más inteligente que sea nunca va a ser más inteligente que todos seres humanos juntos”


ACTIVIDADES:
A continuación, encontraras un cuestionario tipo ICFES, la actividad consiste en construir y desarrollar un plan o estrategia para resolverlos y escoger una de las 4 pociones de respuesta.

1.       Un almacén ofrece una promoción: compre 3 camisetas por $10.000, esto quiere decir que una persona que quiera comprar 15 camisetas debe tener al menos:
A.       $30.000
B.       $40.000
C.       $50.000
D.       $60.000
2.       Un mapa está construido con la siguiente razón: 1cm /1500 metros (un centímetro en el dibujo equivale a 1500 metros en la realidad) Si en la realidad la distancia entre A y B es 9000 metros.
En el mapa esta distancia es:
A.       3 centímetros
B.       6 centímetros
C.       9 centímetros
D.       12 centímetros
3.       La razón entre las edades de Andrés y Beatriz es de 3 a 5, si la edad de Beatriz es 20 años la edad de Andrés es:
A.       12 años
B.       13 años
C.       14 años
D.       15 años

LAS PREGUNTAS 4, 5 y 6, CORRESPONDEN A LA SIGUIENTE TABLA.
En la tabla se registra el número de obreros que se requieren para construir un edificio y los días que emplean para construirlo

Número de obreros
Numero de días
200
30
400
15
600
10
800
X
y
2,5
3000
Z
4.       El valor de” X” es:
A.       7,5 días
B.       8,0 días
C.       8,5 días
D.       9,0 días
5.       El valor de “y “es:
A.       2100 obreros
B.       2200 obreros
C.       2300 obreros
D.       2400 obreros
6.       EL valor de “Z” es:
A.       1 dia
B.       1,5 días
C.       2 días
D.       3 días
7.       Un automóvil realiza el recorrido de la ciudad A a la ciudad B, empleando 6 horas y viajando a una velocidad de 60 kilómetros por hora, si se requiere cubrir la misma distancia en 4 horas, la velocidad a la que debe viajar el auto es:
A.       90 kilómetros por hora
B.       100 kilómetros por hora
C.       120 kilómetros por hora
D.       140 kilómetros por hora
8.       Una piscina la llenan 3 llaves en 15 horas, si dos de ellas se dañan una sola llave la llenara en:
A.       30 horas
B.       35 horas
C.       40 horas
D.       45 horas
9.       Un tubo de 3 metros de largo es cortado en dos secciones cuya razón es de 3 a 7.  Por lo tanto, la medida de la sección más larga tiene:
A.       210 centímetros
B.       220 centímetros
C.       230 centímetros
D.       240 centímetros
10.    En una fiesta se invitaron a niños y niñas. Si sabemos que acudieron en una proporción de 10 niñas por cada 6 niños, y en la fiesta hay 32 niños, la cantidad de niños que acudieron fue:
A.       4 niños
B.       8 niños
C.       12 niños
D.       16 niños



PASATIEMPOS Y PROBLEMAS VARIOS QUE POTENCIAN EL PENSAMIENTO LÓGICO MATEMÁTICO
  1. Un carpintero tiene que cortar un listón de 7 metros de largo, si cada dia corta un metro. ¿cuantos días demorara para cortar los 7 tramos?
  2. Un caracol debe subir una pared de 4 metros, si en la noche sube 2 metros y en el dia baja un metro, ¿cuantos días tarda en ascender los 4 metros?
  3. Dibuje un circulo con un punto en el centro sin levantar la mano ni repetir línea.                                                                    
  4. Cuantas veces se repite el número 1 en los números de 1 hasta 100
  5. Un vendedor de huevos hace su primera venta dando al cliente la mitad de los huevos que lleva en su cesta más medio huevo. Al segundo cliente, le vende la mitad de los huevos que le quedan más medio huevo. Con el tercero hace lo mismo y con el cuarto también. Solo que con el cuarto se queda sin huevos. ¿Con cuántos huevos empezó la venta?

EVALUACIÓN
  1. Responda y describa el proceso que utilizo para hallar la solución de cada uno de los puntos del cuestionario tipo ICFES
  2. De solución a cada uno de los 5 puntos de los pasatiempos y problemas varios que potencian el desarrollo del pensamiento lógico matemático justificando cada respuesta.
  3. Realice una auto evaluación de lo aprendido



FORMULARIO:  Link del formulario de Google https://forms.gle/CPYDMGwMtm2zF8Y



CARTILLA No.2

 

 

COLEGIO MORALBA SUR ORIENTAL I.E.D.

GRADO

6

ASIGNATURA

MATEMÁTICAS

 

 

Guía N°3

 

REALIZAR EN LA SEMANA DEL

28 de septiembre al 16 de octubre de 2020










 INDICADORES DE LOGRO: Resuelve problemas que requieren de la construcción de moldes para cubos, cajas, prismas o pirámides dadas sus dimensiones y justifica cuando cierto molde no resulta válido para la solución de dicha situación.

TEMA: cuerpos geométricos
MARCO TEÓRICO: mira a tu alrededor y veras formas y cuerpos geométricos: un baso en forma de cilindro, un embudo en forma de cono, una caja en forma de prisma, un balón en forma de esfera, un par de dados en forma de cubos. 




Todos los cuerpos geométricos pueden  ser construidos por el ser humano y cumplir funciones determinadas, algunos permiten almacenar líquidos u otras sustancias o simplemente servir de adornos, porque presentan formas especiales sirviendo  de empaques  para regalos.
Todos comparten ciertas características como tener un nombre, poder dibujarse, tener un desarrollo especial, tener un área lateral, tener un volumen.
 
El desarrollo de un cuerpo geométrico se refiere al plano que se dibuja en una hoja para luego recortarse con tijeras, luego armase y pegarse para construir un cuerpo.
 
El área lateral se refiere a la cantidad de unidades cuadradas (centímetros cuadrados o metros cuadrados) que posee el contorno del cuerpo geométrico y que se calculan con base en fórmulas matemáticas específicas
 
El volumen se refiere a  la cantidad de unidades cubicas (cubos) que  contiene en su interior el cuerpo geométrico y que generalmente son centímetros cúbicos o metros cúbicos, el volumen se puede calcular mediante fórmulas matemáticas específicas.
 
Cuando las formas son circulares o los cuerpos son redondos las formulas emplean el número π (se lee numero pi), que es la relación entre la longitud de la circunferencia y su diámetro y que equivale a 3, 1416.

EJEMPLO(S):
A  continuación encontraras una tabla donde están los principales cuerpos geométricos, su desarrollo, la fórmula para calcular el área lateral (A) y el volumen (V), debes observar las letras que se encuentran  en los dibujos y los desarrollos y que corresponden a las medidas específicas  para cada cuerpo geométrico.
El plano del desarrollo se puede utilizar como molde para construir los diferentes cuerpos



 




Ejemplo 1.

Una caja en forma de paralelepípedo, tiene las siguientes dimensiones:

Largo: 20 cm

Ancho: 10 cm

Alto: 15 cm

a.    Hallar el área lateral

b.    Hallar el volumen

Solución: observando la tabla y utilizando las fórmulas para área y volumen.





Identificamos que el valor de “a” es 20 cm, el valor de “b” es 10 cm y el valor de “c” es 15 cm.

El área A  es: 2(ab+ac+bc)

Reemplazando: 2(20x10 + 20x15 + 10x15)=

                           2(200 + 300 + 150)          =

                           2(650)                              =

                            1300 cm2      es el área lateral, es la cantidad de material que se requiere para construir la caja.

Se requieren 1300 cuadrados de  un centímetro de lado.

El volumen  V  es: abc  (largo x ancho x alto)

                              20x10x15 =

                              3000 cm3    es el volumen que tiene la caja.

Caben tres mil cubitos de un cm de arista dentro de la caja.

Ejemplo 2.

Se requiere construir un cilindro cuya base tiene un radio de 10 cm, y una altura de 40 cm.

a.    ¿Cuánto material se requiere, como mínimo?

b.    ¿Qué volumen tiene el interior del cilindro?





Solución:

a.    El área lateral es la cantidad mínima de material que se necesita, según la tabla el área lateral está compuesta por las áreas de las bases, en este caso el área de los dos  círculos de radio 10 cm. Mas el área de un rectángulo cuyo largo es, según la formula, igual a 2πR    y cuya altura es H. reemplazando valores tenemos:

AB= área de una base = πR2  = (3,1416)(10)2=(3,1416)(100)= 314,16

AL= área lateral = 2πRH =2(3,1416)(10)(40)= 2513,28

AT=área total =   2 veces el área de la base más área lateral

                  = 2(314,16) + 2513,28

                  = 628,32 + 2513,28

                  = 3141,6 cm2       se necesitan como mínimo  3141,6 cuadrados de un cm de lado.     

 

b.    El volumen V = ABH  =área de la base por la altura

                     V= (314,16) (40)

                      V= 12566,4 cm3      el volumen del cilindro es de 12566,4 cubos de un cm de lado

Ejemplo 3:

Un cono de helado tiene 8 cm de alto y el radio de la base es de 6 cm.

a.    ¿Cuál es el área lateral?

b.    ¿qué volumen tiene?

Solución:



a.    El área total del cono está compuesta por la suma del área de la base (que es el área de un circulo) más el área lateral.

Para calcular el área lateral tenemos que saber el valor de G (generatriz del cono, este valor se calcula utilizando el teorema de Pitágoras

  Al = AREA LATERAL = ΠRG =3,1416(6)(10)

                                      = 188,496 cm2 

AREA TOTAL=  AB  +    AL  = 113,256 + 188,496

                                            = 301,752 cm2        se necesitan como mínimo 301,752 cuadrados de un cm de lado para forrar el cono de helado.

b.    El volumen del cono así como el de la pirámide es igual a la tercera parte del área de la base por la altura.

 

V= ABH

V=  (π)R2H

V= (3,1416)(62)( 8)

V= 301,5936 cm3   el cono contiene en su interior 301,5936 cubos de un centímetro de arista

 

 

  ACTIVIDADES:

Resolver el siguiente cuestionario tipo icfes, que consta de 6 problemas anexando el proceso que se utilizó para hallar la respuesta, junto con el dibujo del cuerpo y las medidas correspondientes.

1.    Para forrar con plástico, una caja de 30 cm de largo por 20 cm de ancho y 10 cm de alto se requieren como mínimo:

a.    1264 cm2   de plástico

b.    12640 cm2  de plástico

c.    126400 cm2 de plástico

d.    1264000 cm2 de plástico

2.    El volumen de una caja de 30 cm de largo por 20 cm de ancho y 10 cm de alto es:

a.    600 cm3

b.    6000 cm3

c.    260000 cm3

d.    600000 cm3

3.    Para construir un tanque  plástico de forma cilíndrica, de 2 metros de alto y 1 metro de radio de la base, se requiere como mínimo

a.    18,8616 metros cuadrados de plástico

b.    188,616 metros cuadrados de plástico

c.    1886,16 metros cuadrados de plástico

d.    18861,6 metros cuadrados de plástico

4.    El máximo volumen de agua que contiene un tanque cilíndrico de plástico de 2 metros de alto y 1 metro de radio de la base  es:

a.    6,2832 metros cúbicos

b.    62,832 metros cúbicos

c.    628,32 metros cúbicos

d.    6283,2 metros cúbicos

5.    Un cono de 4 cm de alto y un radio de la base de 3 cm tiene una generatriz de:

a.    5 cm

b.    10 cm

c.    15 cm

d.    20 cm

6.    El volumen de un cono de 5 cm de alto y 3 cm de radio de la base está dado por las siguientes operaciones:

a.     π(9)(5)

b.    1/3 π(5)(3)

c.    1/3 π(9)(25)

d.    1/3 π(25)(3)

 

 

CRITERIOS DE EVALUACIÓN

 

1. Responda y describa el proceso que utilizó para hallar la solución de cada uno de los puntos del cuestionario tipo ICFES

2. Realice una autoevaluación de lo aprendido y envíela al docente correspondiente.

Contesta las preguntas cartilla en el siguiente formulario:  

https://forms.gle/rfBqpUkCC9jKWaDc6



 


 

COLEGIO MORALBA SUR ORIENTAL I.E.D.

GRADO

6

ASIGNATURA

MATEMÁTICAS

 Guía N° 4

 


 

REALIZAR EN LA SEMANA DEL

19 de octubre al 6 de noviembre de 2020










 

INDICADORES DE LOGRO: Resuelve problemas que requieren de la construcción de moldes para cubos, cajas, prismas o pirámides dadas sus dimensiones y justifica cuando cierto molde no resulta válido para la solución de dicha situación.

TEMA: construcción de cuerpos geométricos

MARCO TEÓRICO:El uso comprobado de las técnicas de ORIGAMI MODULAR para el desarrollo del pensamiento espacial y geométrico a todo nivel desde preescolar hasta profesional,  permite al estudiante comprender los principios de la geometría euclidiana y aplicar el pensamiento lógico a la vez que aprende a concentrarse en cualquier espacio disponible.

¿Qué se necesita?
Únicamente papel  reciclado, hojas de cuadernos que no se estén utilizando, observación y paciencia.

A continuación vamos a aprender a construir cuerpos geométricos, a partir de la construcción de una sola ficha o modulo, se recomienda aprender el paso a paso de la construcción del módulo y luego  utilizando la lógica armar un cubo o una estrella de ocho puntas.es un proceso parecido al de armar rompecabezas.

Para lo cual recomendamos ver videos relacionados. https://www.youtube.com/watch?v=MpUEE5r-lrY
 
Uno de los módulos más sencillos se denomina módulo Sonobe, y para ello solamente se requiere de utilizar papel cuadrado.
Si no se tiene papel cuadrado sino hojas rectangulares, hay que cortar estas hojas para producir cuadrados iguales, no importa el tamaño del cuadrado  lo único que se requiere es que todos los cuadrados sean del mismo tamaño.

En las papelerías también se consigue el papel ya cortado en tamaños que van desde 5 cm hasta 20 cm, se solicita como papel para origami cuadrado.

Sonobe Modulo paso a paso




Vamos a aprender a crear módulos Sonobe, que nos servirán para montar poliedros de papel. El sistema

Que uso es el habitual, hay matices que he ido cogiendo de varias partes, pero es el módulo básico.

Es muy sencillo de montar y permite realizar todos los poliedros regulares estrellados (de cada cara del

poliedro parte una pirámide triangular)

 

Proceso:
  1. Necesitamos un cuadrado de papel (lo más exacto posible).
  2. Doblamos por la mitad.
  3. Doblamos la mitad del pliegue como se ve en la imagen.
  4. Hacemos lo mismo por la parte de atrás para que quede lo que vemos en la foto.
  5. Desplegamos y, dejando el cuadrado como se ve en la imagen, doblamos las esquinas (es importante que sean siempre las mismas, porque sino luego los módulos no encajarán).
  6. Este paso no es necesario, yo lo he tomado de la página de Jordi Mas, y me gusta porque el módulo queda más consistente.
  7. Volvemos a doblar los pliegues laterales.
  8. Tal y como lo tenemos encima de la mesa doblamos las esquinas como se ve en la imagen (es importante no hacerlo al revés porque si no no podemos hacer el siguiente paso).
  9. Metemos los pliegues dentro de los “bolsillos” para que quede compacto.
  10. Le damos la vuelta.
  11. Tal y como aparece en la imagen número 10, levantamos las esquinas para que aparezca
  12. como en la 11 (Hay que fijarse bien porque es fácil hacerlo al revés).
  13. Doblamos por el eje central y ya tenemos el módulo terminado, ahora tendremos que hacer
  14. varios (como mínimo tres) para poder montar alguna figura.

Fuentes.  http://ccoblog.wordpress.com

Armado del cubo



 

 

 


CRITERIOS DE EVALUACIÓN
1. Con cuadrados de 10 cm construya  6 módulos tipo sonobe, arme  un cubo. Calcule el área lateral  y el volumen del cubo construido

2. Con cuadrados de 10 cm  construya 12 módulos tipo sonobe, arme una estrella de 8 puntas. Calcule el área lateral y el volumen de la estrella de ocho puntas (octaedro)  construida. Para armar la estrella puede ver el siguiente video:
https://www.youtube.com/watch?v=GlPQ2XQk-dc

3. Envíe foto del cubo, la estrella de 8 puntas y su nota de autoevaluación de la materia. Whatssapp 3195327700
 
PLAN DE MEJORAMIENTO FINAL
1. MEDICIÓN DE ÁNGULOS:      
Entra al siguiente link, mide los 20 ángulos que se te presentan, con ayuda del transportador que allí aparece, al final envía foto  la nota  que te sale. Puedes volver a repetirlo hasta completar el 100% envíala por el Whatsapp 3195327700
https://www.thatquiz.org/es/practicetest?8y3upjsyr0r

2. TANGRAM VIRTUAL
Entra al siguiente link,  realiza 10 ejercicios del TANGRAM VIRTUAL, colócalos en 1 hoja de Word tamaño oficio, tómale una foto y envíala por el Whatsapp 3195327700
 
https://www.geogebra.org/m/QFc9jN6P.

3. FIGURA DE ÁNGULOS.


Entra al siguiente link, realiza la imagen que se te presenta Un lobo, o la que tu desees, utiliza el programa geogebra para ello, que te permite coloréala, tómale foto y envíala por el Whatsapp 3195327700.


 



¡NOTA IMPORTANTE¡

Las actividades anteriores son lúdicas se realizan en línea, el link de cada uno te da el ingreso y te permite realizarlas.

Si no tienes conexión a internet, puedes hacerlo manual ó algunas en línea y otras manual y me envía la foto de cada actividad. Son solo 3 actividades, recibo solamente 3 fotos, bien organizadas por favor.

¡Inténtalo y diviértete¡

 




CARTILLA TERCER 

Clic aqui para ver o descargar



Solamente si no tienes TEAMS, puedes ingresar al formulario del taller No. 1 por acá:

Dale click  si eres de 601 


Dale click si eres 602






PLAN DE MEJORAMIENTO TERCER TRIMESTRE.


Docente: MARITZA MAYOR LÓPEZ   Jornada: MAÑANA Sede: A

Grado: SEXTO   Asignatura: MATEMÁTICAS.

Teniendo en cuenta los resultados académicos del tercer trimestre, se proponen las siguientes acciones y actividades de mejoramiento; las cuales se desarrollarán durante la semana del 8 al 12 noviembre 2021.

Logros con dificultades y que no han sido alcanzados:

 

 

·         Resolver y formular problemas sencillos de proporcionalidad directa

·         Hace traducciones entre diferentes representaciones de un conjunto de datos para dar solución a un problema

·         Resuelve problemas que requieren de la construcción de moldes para cubos, cajas, prismas o pirámides dadas sus dimensiones y justifica cuando cierto molde no resulta válido para la solución de dicha situación.

 

Actividad de mejoramiento: actividad(es) lúdicas a presentar a los estudiantes:

 

Teniendo en cuenta la información de la cartilla, los apuntes de clase y las explicaciones del docente; los estudiantes pondrán en práctica los conceptos vistos según los logros establecidos y resolverán una actividad lúdica por quizziz.

Herramientas y/o recursos a utilizar:

Recursos tecnológicos para el envío de las actividades.

Cartilla tercer trimestre.

Cuaderno con apuntes.

Tener en el cuaderno copiados o impresos formularios 1,2, y 3

Tiempo estimado para abordar la actividad:

30 minutos

Criterios de evaluación:

Entrar al siguiente link y contestar las preguntas:

https://quizizz.com/join?gc=00152769

 

 

Aclaraciones:

·         Vence 12 de noviembre

·         Puede repetirlo las veces que desee.

·         Es un juego en línea.

·         Consta de 15 preguntas y serán tomadas de los 3 formularios trabajados durante el tercer trimestre.

Indicaciones y/o recomendaciones sobre entrega de actividades:

Enviar (1) foto por tareas de teams del % obtenido en la actividad juego de quizziz

·         Si sacó 100% de la actividad, equivale a 3,5

·         95% equivale a 3.3

·         90% equivale a 3,1 y así sucesivamente.

 

Cordialmente

Docente de Matemáticas





PLAN DE MEJORAMIENTO FINAL MATEMÁTICAS 

Docente: MARITZA MAYOR LÓPEZ   Jornada: MAÑANA Sede: A

Grado: SEXTO   Asignatura: MATEMÁTICAS.

Teniendo en cuenta los resultados académicos, FINALES  se proponen las siguientes acciones y actividades de mejoramiento

Herramientas y/o recursos a utilizar:

Recursos tecnológicos para el envío de las actividades.

Cartilla tercer trimestre.

Cuaderno con apuntes.


Tiempo estimado para abordar la actividad:

30 minutos

Criterios de evaluación:

Entrar al siguiente link y contestar las preguntas:

https://quizizz.com/join?gc=63554017

Aclaraciones:

·         Vence 20 de noviembre

·         Puede repetirlo las veces que desee.

·         Es un juego en línea.

  


TALLER DE INTELIGENCIA EMOCIONAL









GRADO SÉPTIMO


LINKS DE APOYO - OPERACIONES REGLA DE LOS SIGNOS PARA SUMAS Y RESTAS


No hay comentarios:

Los comentarios nuevos no están permitidos.

Suscribirse a: Entradas (Atom)